题目
已上传洛谷:U605360 最小交通费
有一个圆上均匀分布着L个点(编号按逆时针顺序依次为1~L)。在这些点中还存在m条弦。如果在圆弧上从一个点走到另一个相邻的点,需要支付1元的费用;但如果通过弦来走(包括交点),则无需支付费用。
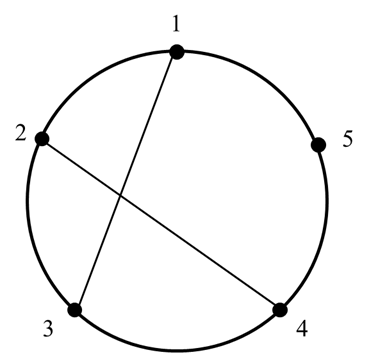
例如,如图所示,如果存在弦(1,3)和(2,4),则从点1到点2可以先从1走到两条弦的交点,再从交点走到2,这样就无需收费。请你设计算法,找出某两个点之间最少的交通费。
- 程序的第一行输入三个整数:L、m、q,用空格分隔。
- 接下来输入m行,每行两个整数,表示一条弦。
- 接下来输入q行,每行两个整数,表示q个问题。如“1 2”则表示一个问题,表示点1和2之间的最少交通费。
- 程序的输出为q行,每行为一个问题的答案。
注:题中 L 最大为 3 × 10^8
示例输入
15 2 1
21 3
32 4
41 2
示例输出
10
机试情况
南软/智软的夏令营机试是4小时4道题,每题100分,满分400分。4小时内排行榜上此题无人AC,不过有人拿到60-70分。我自己在考场也是只拿到部分分数(没想到通法,只打表了一些少数点的情况),事后思考后才成功解决。
解题思路
我们可以自然地把这个问题抽象为一个图,其中包含两种不同代价的边:
- 圆弧边:连接圆上相邻的两个点,例如点 i 和点 i+1(以及点 L 和点 1)。走这些边需要花费1元,因此它们的边权为 1。
- 免费边:所有通过弦和弦的交点构成的路径。走这些边无需花费,因此它们的边权为 0。
问题的关键在于,所有通过弦和交点能够互相到达的点,实际上构成了一个“免费交通网络”。网络内的任意两点之间都可以零费用到达。我们可以把这样一个网络视为一个连通分量。
所以我们可以用并查集 来高效地处理和合并这些连通分量。
- 初始化:将圆上的
L个点每一个都看作一个独立的集合。 - 合并弦端点:对于给定的
m条弦,每条弦(u, v)都意味着u和v是零费用连通的。我们将u和v所在的集合合并。 - 合并相交弦:接下来,我们需要找出所有相交的弦。
- 如何判断两条弦是否相交? 假设有两条弦
(a, b)和(c, d)。为了方便判断,我们先将每条弦的端点按编号从小到大排序,即u1 = min(a, b), v1 = max(a, b)和u2 = min(c, d), v2 = max(c, d)。 这两条弦在圆内相交的充要条件是,它们的端点在圆上是交错排列的。也就是说,必须满足u1 < u2 < v1 < v2或者u2 < u1 < v2 < v1。 - 对于每一对相交的弦,例如
(a, b)和(c, d),它们的所有四个端点a, b, c, d都应该在同一个零费用连通分量中。我们只需将其中任意一个点(如a)与另一条弦的任意一个点(如c)所在的集合合并即可。
- 如何判断两条弦是否相交? 假设有两条弦
完成以上步骤后,并查集就完整地记录了所有的零费用连通分量。
第二步:计算两个点之间的最短交通费
对于每一个查询 (s, t):
- 首先,我们使用并查集的
find操作检查s和t是否在同一个连通分量中。- 如果
find(s) == find(t),说明它们在同一个免费交通网络内,可以直接到达,费用为 0。
- 如果
- 如果它们不在同一个连通分量中,费用就来自于在圆弧上从一个连通分量“跳”到另一个连通分量的次数。这可以转化为一个在 “分量图” 上的最短路问题。
- 图中的每个节点代表一个连通分量。
- 如果圆弧上相邻的两个点
i和i+1属于不同的连通分量(即find(i) != find(i+1)),我们就在这两个分量对应的节点之间连一条边,权重为 1。 - 问题就变成了,在分量图上,从
s所在的分量走到t所在的分量,最少需要经过几条边。这是一个典型的无权图最短路问题,可以使用BFS 来解决。
C++ 代码
1#include <iostream>
2#include <vector>
3#include <numeric> // iota
4#include <algorithm> // swap, min, max
5#include <utility> // pair
6#include <map>
7#include <queue>
8
9using namespace std;
10
11// -------- DSU 模板 --------
12class DSU
13{
14public:
15 vector<int> parent;
16 vector<int> sz; // 按大小合并的依据 (避免与C++的size()函数重名,改为sz)
17 int count; // 联通分量
18 DSU(int n)
19 {
20 count = n;
21 parent.resize(n);
22 sz.resize(n);
23 iota(parent.begin(), parent.end(), 0); // 从0开始连续填充
24 sz.assign(n, 1);
25 }
26 int find(int i)
27 {
28 if (parent[i] == i)
29 return i;
30 return parent[i] = find(parent[i]);
31 }
32 void unite(int a, int b)
33 {
34 int root_a = find(a), root_b = find(b);
35 if (root_a != root_b)
36 {
37 if (sz[root_a] < sz[root_b])
38 std::swap(root_a, root_b);
39 // a是大树,b合并到a
40 parent[root_b] = root_a;
41 sz[root_a] += sz[root_b];
42 count--;
43 }
44 }
45 bool is_connected(int a, int b)
46 {
47 return find(a) == find(b);
48 }
49 // 获取联通分量
50 int get_count() const
51 {
52 return count;
53 }
54 // 获取i所在集合的大小
55 int get_size(int i)
56 {
57 return sz[find(i)];
58 }
59};
60// -------- DSU 模板结束 --------
61
62
63int main()
64{
65 // C++ 标准输入输出加速
66 ios_base::sync_with_stdio(false);
67 cin.tie(NULL);
68
69 int L, m, q;
70 cin >> L >> m >> q;
71
72 // --- 步骤 1: 预处理,构建零费用连通分量 ---
73
74 // DSU对象,大小为L+1以方便使用1-based索引
75 DSU dsu(L + 1);
76
77 vector<pair<int, int>> chords;
78 for (int i = 0; i < m; ++i)
79 {
80 int u, v;
81 cin >> u >> v;
82 // 存储弦,并保证端点有序,方便后续判断
83 chords.push_back({std::min(u, v), std::max(u, v)});
84 // 合并弦的两个端点
85 dsu.unite(u, v);
86 }
87
88 // 检查所有弦的配对,看它们是否相交 (O(m^2))
89 for (int i = 0; i < m; ++i)
90 {
91 for (int j = i + 1; j < m; ++j)
92 {
93 int u1 = chords[i].first;
94 int v1 = chords[i].second;
95 int u2 = chords[j].first;
96 int v2 = chords[j].second;
97
98 // 判断相交:端点是否交错排列
99 // (u1 < u2 < v1 < v2) 或 (u2 < u1 < v2 < v1)
100 if ((u1 < u2 && u2 < v1 && v1 < v2) || (u2 < u1 && u1 < v2 && v2 < v1))
101 {
102 // 如果相交,合并它们所在的集合
103 // 只需要合并任意两个不同弦上的点即可
104 dsu.unite(u1, u2);
105 }
106 }
107 }
108
109 // --- 步骤 2: 构建“分量图” ---
110
111 // 使用 map 将 DSU 的根节点映射到从 0 开始的连续索引
112 map<int, int> comp_map;
113 int comp_idx_counter = 0;
114 for (int i = 1; i <= L; ++i) {
115 int root = dsu.find(i);
116 if (comp_map.find(root) == comp_map.end()) {
117 comp_map[root] = comp_idx_counter++;
118 }
119 }
120
121 int num_components = comp_map.size();
122 vector<vector<int>> comp_adj(num_components);
123
124 // 遍历圆周上的所有相邻点对,构建分量图的邻接表
125 for (int i = 1; i <= L; ++i)
126 {
127 int p1 = i;
128 int p2 = (i == L) ? 1 : i + 1; // p2是p1在圆上的下一个点
129
130 // 如果相邻点属于不同分量,则在分量图上添加一条边
131 if (!dsu.is_connected(p1, p2))
132 {
133 int root1 = dsu.find(p1);
134 int root2 = dsu.find(p2);
135 int idx1 = comp_map[root1];
136 int idx2 = comp_map[root2];
137 comp_adj[idx1].push_back(idx2);
138 comp_adj[idx2].push_back(idx1);
139 }
140 }
141
142 // --- 步骤 3: 处理查询 ---
143 for (int i = 0; i < q; ++i)
144 {
145 int s, t;
146 cin >> s >> t;
147
148 // 如果起点和终点在同一个分量,费用为0
149 if (dsu.is_connected(s, t))
150 {
151 cout << 0 << "\n";
152 continue;
153 }
154
155 // 否则,在分量图上运行BFS
156 int start_comp_idx = comp_map[dsu.find(s)];
157 int end_comp_idx = comp_map[dsu.find(t)];
158
159 queue<pair<int, int>> bfs_q; // 存储 {当前分量索引, 距离}
160 vector<int> dist(num_components, -1); // -1表示未访问
161
162 bfs_q.push({start_comp_idx, 0});
163 dist[start_comp_idx] = 0;
164
165 while (!bfs_q.empty())
166 {
167 auto [curr_comp, d] = bfs_q.front();
168 bfs_q.pop();
169
170 if (curr_comp == end_comp_idx)
171 {
172 cout << d << "\n";
173 break;
174 }
175
176 for (int neighbor_comp : comp_adj[curr_comp])
177 {
178 if (dist[neighbor_comp] == -1) // 如果邻居未被访问
179 {
180 dist[neighbor_comp] = d + 1;
181 bfs_q.push({neighbor_comp, d + 1});
182 }
183 }
184 }
185 }
186
187 return 0;
188}
补充:优化思路
由于题目给出的 L 最大可达 3 * 10^8,上面代码会导致MLE。DSU dsu(L + 1) 至少需要约 2.4 GB 内存,显然是不可接受的。
解决这个问题的核心思想是离散化,也称关键点法。我们无需关心圆上所有的 L 个点,真正影响“免费交通网络”结构和连接性的,只有那些被明确提到的“关键点”。
这些“关键点”包括:
- 所有
m条弦的2*m个端点。 - 所有
q次查询的2*q个起点和终点。
除此之外的所有其他点,我们都可以看作是“空白”的弧。我们只需处理这数量级很小(最多 2m + 2q 个)的关键点,并计算它们之间的关系即可。
对原算法进行如下两个关键的改造:
- 使用基于
std::map的并查集(DSU)。 我们将 DSU 的底层实现从std::vector改为std::map。map只会为我们实际接触到的“关键点”动态分配内存,而不会预先分配一个大小为 L 的巨大数组。这直接将空间复杂度从O(L)降至O(m+q)。 - 高效构建带权的“分量图”并使用Dijkstra算法。我们不再遍历
1到L来建图,而是只关注由所有关键点分割出的关键弧。- 首先,我们将所有关键点收集起来,并进行排序和去重。
- 然后,我们遍历这个排好序的关键点列表。对于每一对在圆弧上相邻的关键点(例如列表中的
p_i和p_{i+1},以及最后一个点和第一个点形成的环形弧),它们之间就构成了一段关键弧。 - 如果这段弧两端的关键点
p_i和p_{i+1}属于不同的连通分量(即find(p_i) != find(p_{i+1})),那么这段弧就是连接两个免费区的“付费桥梁”。 - 关键修正一: 我们就在这两个分量对应的节点之间连一条边。这条边的权重并非固定的1,而是这段弧的实际长度(例如
p_{i+1} - p_i)。 - 关键修正二: 因为边的权重不同,使“分量图”成为一个带权图。因此,在求解两个分量间的最短路时,我们必须使用 Dijkstra 算法,而非原思路中的 BFS。
这样,我们就在时间和空间上都高效地解决了这个问题。算法复杂度只与 m 和 q 的大小相关,而与巨大的 L 无关。
C++ 代码
1#include <iostream>
2#include <vector>
3#include <algorithm>
4#include <utility>
5#include <map>
6#include <queue>
7#include <set>
8
9using namespace std;
10
11// -------- 基于 map 的 DSU 模板 --------
12class MapDSU {
13public:
14 map<int, int> parent;
15 map<int, int> sz;
16
17 int find(int i) {
18 if (parent.find(i) == parent.end()) {
19 parent[i] = i;
20 sz[i] = 1;
21 }
22 if (parent[i] == i) {
23 return i;
24 }
25 return parent[i] = find(parent[i]);
26 }
27
28 void unite(int a, int b) {
29 int root_a = find(a);
30 int root_b = find(b);
31 if (root_a != root_b) {
32 if (sz[root_a] < sz[root_b]) {
33 swap(root_a, root_b);
34 }
35 parent[root_b] = root_a;
36 sz[root_a] += sz[root_b];
37 }
38 }
39
40 bool is_connected(int a, int b) {
41 // find会自动初始化不存在的点
42 return find(a) == find(b);
43 }
44};
45
46const long long INF = 1e18;
47
48int main() {
49 ios_base::sync_with_stdio(false);
50 cin.tie(NULL);
51
52 long long L;
53 int m, q;
54 cin >> L >> m >> q;
55
56 MapDSU dsu;
57 vector<pair<int, int>> chords(m);
58 set<int> key_points_set;
59
60 // --- 步骤1: 合并弦和相交弦 ---
61 for (int i = 0; i < m; ++i) {
62 cin >> chords[i].first >> chords[i].second;
63 if (chords[i].first > chords[i].second) {
64 swap(chords[i].first, chords[i].second);
65 }
66 dsu.unite(chords[i].first, chords[i].second);
67 key_points_set.insert(chords[i].first);
68 key_points_set.insert(chords[i].second);
69 }
70
71 for (int i = 0; i < m; ++i) {
72 for (int j = i + 1; j < m; ++j) {
73 long long u1 = chords[i].first, v1 = chords[i].second;
74 long long u2 = chords[j].first, v2 = chords[j].second;
75 if (u1 > u2) {
76 swap(u1, u2); swap(v1, v2);
77 }
78 if (u1 < u2 && u2 < v1 && v1 < v2) {
79 dsu.unite(u1, u2);
80 }
81 }
82 }
83
84 // --- 步骤2: 收集所有关键点 ---
85 vector<pair<int, int>> queries(q);
86 for (int i = 0; i < q; ++i) {
87 cin >> queries[i].first >> queries[i].second;
88 key_points_set.insert(queries[i].first);
89 key_points_set.insert(queries[i].second);
90 }
91
92 vector<int> key_points(key_points_set.begin(), key_points_set.end());
93
94 // --- 步骤3: 构建带权的“分量图” ---
95 map<int, int> root_to_idx; // DSU根节点到分量图新索引的映射
96 int comp_idx_counter = 0;
97 for (int point : key_points) {
98 int root = dsu.find(point);
99 if (root_to_idx.find(root) == root_to_idx.end()) {
100 root_to_idx[root] = comp_idx_counter++;
101 }
102 }
103
104 int num_components = root_to_idx.size();
105 // 邻接表存储 {邻居分量索引, 权重}
106 vector<vector<pair<int, long long>>> comp_adj(num_components);
107
108 // 只需检查排序后相邻关键点之间的弧
109 for (size_t i = 0; i < key_points.size(); ++i) {
110 int p1 = key_points[i];
111 // p2 是 p1 在关键点列表中的下一个点(包括环形)
112 int p2 = key_points[(i + 1) % key_points.size()];
113
114 int root1 = dsu.find(p1);
115 int root2 = dsu.find(p2);
116
117 if (root1 != root2) {
118 long long dist;
119 if (i == key_points.size() - 1) { // 最后一个点到第一个点的环形距离
120 dist = (L - p1) + p2;
121 } else {
122 dist = p2 - p1;
123 }
124 int idx1 = root_to_idx[root1];
125 int idx2 = root_to_idx[root2];
126 comp_adj[idx1].push_back({idx2, dist});
127 comp_adj[idx2].push_back({idx1, dist});
128 }
129 }
130
131 // --- 步骤4: 处理查询 ---
132 for (const auto& query : queries) {
133 int s = query.first;
134 int t = query.second;
135
136 if (dsu.is_connected(s, t)) {
137 cout << 0 << "\n";
138 continue;
139 }
140
141 int start_root = dsu.find(s);
142 int end_root = dsu.find(t);
143 int start_idx = root_to_idx[start_root];
144 int end_idx = root_to_idx[end_root];
145
146 // Dijkstra 算法
147 priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<pair<long long, int>>> pq;
148 vector<long long> dist(num_components, INF);
149
150 dist[start_idx] = 0;
151 pq.push({0, start_idx});
152
153 while (!pq.empty()) {
154 auto [d, u] = pq.top();
155 pq.pop();
156
157 if (d > dist[u]) continue;
158 if (u == end_idx) break;
159
160 for (const auto& edge : comp_adj[u]) {
161 int v = edge.first;
162 long long weight = edge.second;
163 if (dist[u] + weight < dist[v]) {
164 dist[v] = dist[u] + weight;
165 pq.push({dist[v], v});
166 }
167 }
168 }
169 cout << dist[end_idx] << "\n";
170 }
171
172 return 0;
173}